ガモフによる「アルキメデスの原理」の証明
October 6, 2008 – 4:51 pm最近、私の本棚に眠っていたガモフ全集を少しずつ読んでいる。ガモフは、アルファ崩壊を「トンネル効果」で説明したことで知られる高名な物理学者だ。物理学者本来の姿に加えて、難解な物理理論を「平易」に解説した数多くの一般向け著作を残していることでも有名だ。このガモフの著作を集めたのがガモフ全集、全12巻と別巻3冊として日本語訳が出版されている。この全集、ほぼ40年前に、私が学生時代に購入したものだ。この本を読んでいて、最近、話題にされている理科離れの理由に思いいたることがあった。
ガモフ全集第10巻「物理の伝記」: ここで話題にするのは、ガモフ全集のなかの第10巻「物理の伝記」(鎮目泰夫訳/白揚社刊)の「アルキメデスの原理」の部分だ。この「物理の伝記」では、物理学上の諸発見を「古代ギリシャ」から原子核・素粒子理論にいたるまで連続した物語として「平易」に説明している。「平易」といっても、私にとっては、その内容を完全にフォローすることはできない。しかし、少なくとも、理解したような気分にしてくれる。このあたりが、この本の凄いところだ。
アルキメデスの原理: この本の最初のほうに、アルキメデスの原理(本書では、「アルキメデスの浮体の法則」となっている)がでてくる。アルキメデスの原理は、誰でも知っている「任意の固体は液体にひたされると、それがおしのけた液体の重さだけ軽くなる」という原理だ。さて、この原理・法則は、どのように証明されるのか? 考えてみると、結構、難しい。ガモフは、この原理を次のように説明する(以下、抜粋):
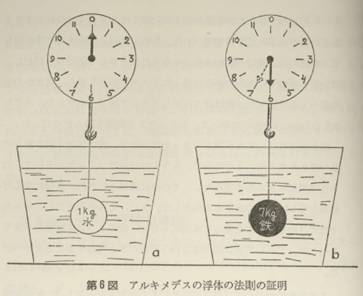
アルキメデス自身がその著<浮体について>で与えたアルキメデスの法則の証明は、完全に正しくはあるが、かなりまわりくどいので、ここではそれをもっと近代的なことばで言いかえて、もしわれわれが中空でない金属球をバケツの中にひたしたらどうなるかを考えてみよう(第6図)。まず、鉄の球のかわりに、同じ直径のうすいプラスチックの球を水にみたしたもの(第6図a)を考えよう。プラスチックの球殻の重さは無視できるから、この場合の状況は、球殻内の水がバケツの中の水の一部である場合と同じであり、ハカリの針はゼロを示す。つぎに、球殻内の水を鉄でおきかえよう(第6図b)。鉄は等容積の水の7倍の重さがある。1Kgの水はバケツの中の周囲の水にささえられて針がゼロを示すから、水を鉄でおきかえれば7-1=6kgだけ重みが加わり、針は6kgを指すはずである。したがって、重さが(空気中で)7kgの鉄球は、水中にひたされると、それがおしのけた水の重さである1kgだけ軽くなる。これがアルキメデスの法則である。すなわち、任意の固体は液体にひたされると、それがおしのけた液体の重さだけ軽くなる。(p.39-40)
この説明、ガモフが考えたものかどうかは知らない。しかし、物理現象を理解するときの基本を教えてくれるように感じるのは私一人か?科学リテラシーという話が話題になるが、このあたりが重要になるのではないかと思うのだ。的外れな表現になるのかもしれないが、この説明、ある種の「思考実験」の原型といったものが示されていると思う。
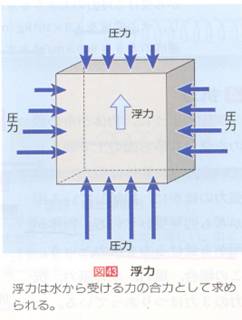
高校の「物理」ではどのように説明されているか?: 私には、高校1年になる娘がいる。物理の時間に「浮力」を教わったようだ。この浮力の説明が終わったところで、「アルキメデスの原理」が紹介されている。どのように説明されているのか?娘の教科書では、まず、「浮力」について説明され、それに続いて、「アルキメデスの原理」が「紹介」されている。「浮力」の説明は、下図にしめされるように、「浮力は水から受ける力の合力として求められる。」として立方体の上部と下部の圧力差として説明される。この説明に先立って、「圧力」、「密度」などなどが説明されている。これらの概念を理解したのちにやっと「浮力」が説明され、そして有名な「アルキメデスの原理」の紹介に至るわけだ。
どちらの説明が良い説明か?ということになると、どちらの説明も良い説明ということになる。どちらも大切だ。ただ、ガモフの「証明」には、特別な知識、準備を必要としない。これに対して、高校の教科書では、「アルキメデスの原理」に至るまでにかなりの準備が必要だ。
さらに、ガモフの方法では固体の形状がなんであれ、なんの困難もなく説明できてしまう。これに対し、高校の教科書で用いている方法では、固体の形状が変わる、例えば立方体から球体に変わっただけで、浮力を実際に求め、「アルキメデスの原理」が成立することを導くのは容易ではない。
物理を学ぶ楽しさということを考えると、ガモフの「証明」で行われているある種の「思考実験」ということの大切さ、パワーをもっと取り入れた方がよいのではないかと思う。「物理の伝記」全体を通じて、物理学の発展にとって、こうした「思考実験」の力、重要性が説かれているように感じる。実は、物理を学ぶ楽しさは、このあたりになるのではないかと思うのだ。このあたりが科学離れの傾向を阻止するうえで、重要な視点と思うのであるが、いかがだろうか?数式を操作するだけが、物理学ではないのだ(数式を操作する重要性は否定すべきではないのはもちろんのことであるのだが・・)。
1 Trackback(s)